538. 把二叉搜索树转换为累加树 (opens new window)

题目：

给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

• 节点的左子树仅包含键 小于 节点键的节点。
• 节点的右子树仅包含键 大于 节点键的节点。
• 左右子树也必须是二叉搜索树。

注意： 本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同

示例：

示例 1：

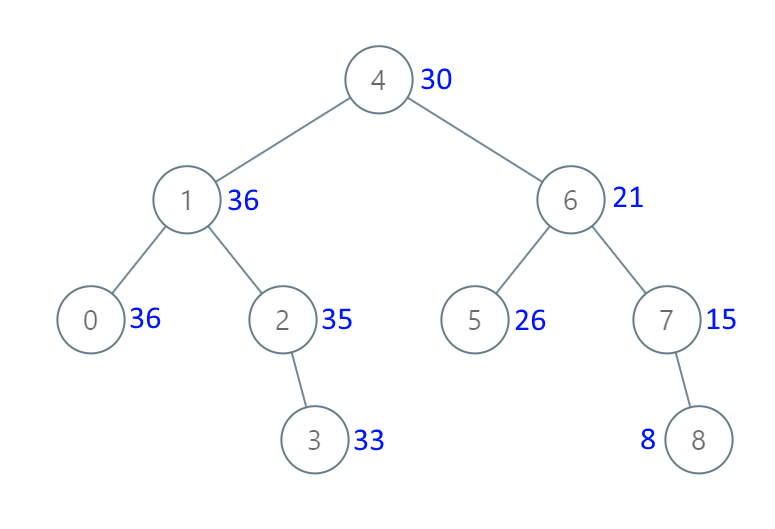
输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

题目解释：

是不是没读懂题目？没关系，举个例子你就明白了：

比如说根节点4转换为累加树之后为什么新值是30？按题目中的意思就是大于等于根节点4的原来二叉树的值全部加起来，即根节点4+（它的右子树）= 4 + 6 + 5 + 7 + 8 = 30，同理根节点4的左孩子节点1，那就是要将大于等于1的原二叉树的值全部加起来，那就是从自身开始1 + 2 + 3 + （之前根节点4累加的值，因为它们都比1大） = 36，所以新值为36，依此类推。

这样子看来，题目是读懂了，但是没啥规律啊？解不了题啊？

根据题目的提示会发现原二叉树是满足以下性质的：

1. 若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
2. 若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
3. 它的左、右子树也分别为二叉搜索树。

说明原二叉树就是二叉搜索树，而累加树则刚好与二叉搜索树性质相反，刚好二叉搜索树的中序遍历是一个单调递增的有序序列。那么是否意味着累加树的逆序中序遍历是一个单调递减的有序序列。

二叉搜索树的中序遍历：[0、1、2、3、4、5、6、7、8]

累加树的中序遍历：[36、36、35、33、30、26、24、15、8]

果然如此！

示例 2：

输入：root = [0,null,1]
输出：[1,null,1]

示例 3：

输入：root = [1,0,2]
输出：[3,3,2]

示例 4：

输入：root = [3,2,4,1]
输出：[7,9,4,10]

提示：

• 树中的节点数介于 0 和 104 之间。
• 每个节点的值介于 -104 和 104 之间。
• 树中的所有值 互不相同 。
• 给定的树为二叉搜索树。

解题：

方法一：反序中序遍历

所以根据我的题目解释，这样我们只需要反序中序遍历该二叉搜索树，记录过程中的节点值之和，并不断更新当前遍历到的节点的节点值，即可得到题目要求的累加树。

class Solution {
public:
    int sum = 0;
    TreeNode* convertBST(TreeNode* root) {
        if(root != nullptr) {
            convertBST(root->right);
            sum += root->val;
            root->val = sum;
            convertBST(root->left);
        }
        return root;
    }
};

复杂度分析：

• 时间复杂度：O(n)，其中 n 是二叉搜索树的节点数。每一个节点恰好被遍历一次。

• 空间复杂度：O(n)，为递归过程中栈的开销，平均情况下为 O(log~⁡n~)，最坏情况下树呈现链状，为 O(n)。

看不懂代码的可以去调试一下代码就懂了

#include <iostream>

// 二叉树节点定义
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

class Solution {
public:
    TreeNode* convertBST(TreeNode* root) {
        if(root != nullptr) {
            convertBST(root->right);
            sum += root->val;
            root->val = sum;
            convertBST(root->left);
        }
        return root;
    }

private:
    int sum = 0; // 成员变量用于记录累加值
};

// 中序遍历打印二叉树
void inOrderTraversal(TreeNode* root) {
    if (root) {
        inOrderTraversal(root->left);
        std::cout << root->val << " ";
        inOrderTraversal(root->right);
    }
}

int main() {
    // 示例用法
    // 创建一棵示例二叉搜索树
    TreeNode* root = new TreeNode(4);
    root->left = new TreeNode(1);
    root->right = new TreeNode(6);
    root->left->left = new TreeNode(0);
    root->left->right = new TreeNode(2);
    root->right->left = new TreeNode(5);
    root->right->right = new TreeNode(7);
    root->left->right->right = new TreeNode(3);
    root->right->right->right = new TreeNode(8);


    // 创建 Solution 对象
    Solution solution;

    // 转换为累加树（使用你提供的方式）
    TreeNode* greaterSumTree = solution.convertBST(root);

    // 打印累加树的中序遍历结果
    std::cout << "累加树的中序遍历结果: ";
    inOrderTraversal(greaterSumTree);
    std::cout << std::endl;

    return 0;
}

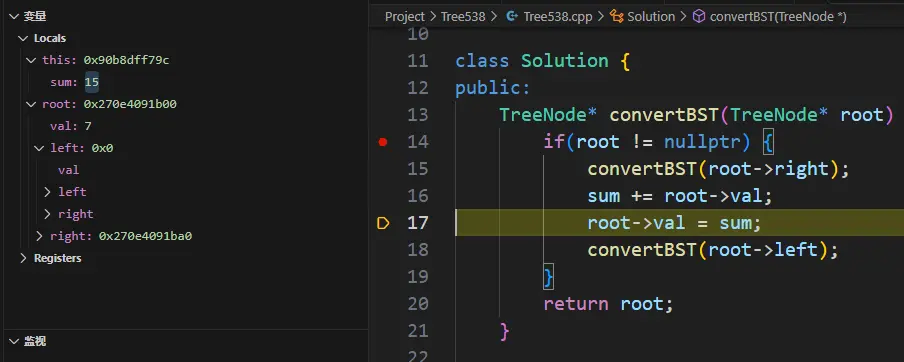
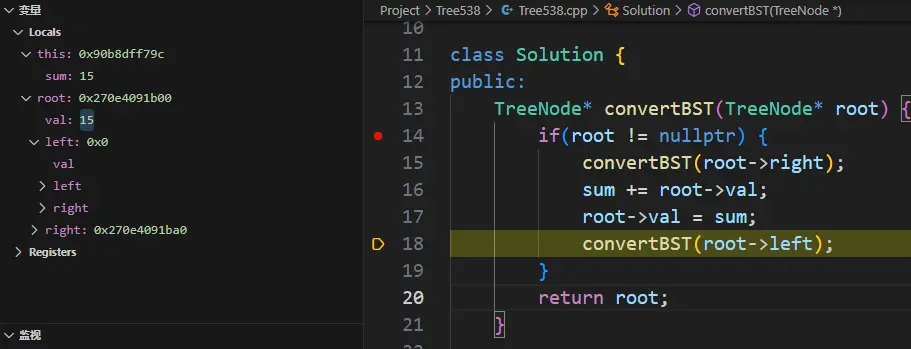
下面给出部分调试过程：

一开始先一直递归，直到右子树的末尾叶子节点8

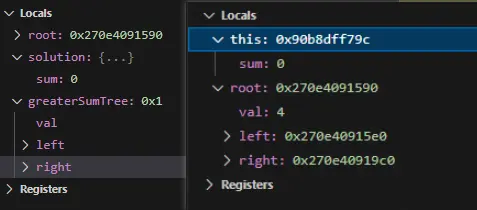
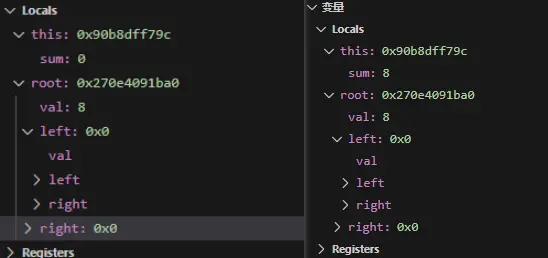
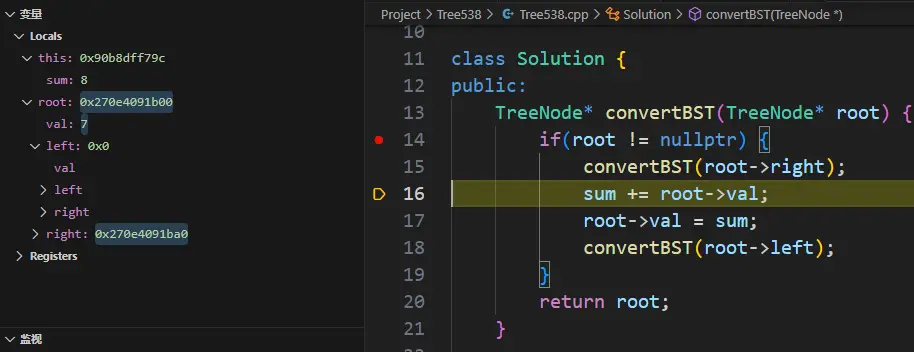
然后递归里的执行：

方法二：Morris 遍历

这个方法不搞了，第一个理解透彻就挺累的了。有需要自己去看吧

538. 把二叉搜索树转换为累加树 - 力扣（LeetCode） (opens new window)