234. 回文链表 (opens new window)

题目：

给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。如果是，返回 true ；否则，返回 false 。

示例：

示例 1：

输入：head = [1,2,2,1]
输出：true

示例 2：

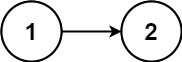
输入：head = [1,2]
输出：false

提示：

• 链表中节点数目在范围[1, 105] 内
• 0 <= Node.val <= 9

**进阶：**你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题？

解题：

方法一：在数组中使用双指针法 时间=空间O(n)

把单链表中的值复制到数组中，然后使用双指针法，一头一尾相向遍历。这需要 O(n) 的时间，因为访问每个元素的时间是 O(1)，而有 n 个元素要访问。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    bool isPalindrome(ListNode* head) {
        vector<int> values;
        while(head != nullptr) {
            values.emplace_back(head->val);
            head = head->next;
        }
        for(int i = 0, j = (int)values.size() - 1; i < j; ++i,--j) {
            if(values[i] != values[j]) {
                return false;
            }
        }
        return true;
    }
};

复杂度分析：

• 时间复杂度：O(n)，其中 n 指的是链表的元素个数。
  • 第一步： 遍历链表并将值复制到数组中，O(n)。
  • 第二步：双指针判断是否为回文，执行了 O(n/2) 次的判断，即 O(n)。
  • 总的时间复杂度：O(2n)=O(n)。
• 空间复杂度：O(n)，其中 n 指的是链表的元素个数，我们使用了一个数组列表存放链表的元素值。

---

方法二：递归 时间=空间=O(n)

使用递归反向迭代节点，同时使用递归函数外的变量向前迭代，就可以判断链表是否为回文。算法的正确性在于递归处理节点的顺序是相反的，而我们在函数外又记录了一个变量，因此从本质上，我们同时在正向和逆向迭代匹配。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
    ListNode* frontPointer;
public:
    bool recursivelyCheck(ListNode* currentNode) {
        if(currentNode != nullptr) {
            if(!recursivelyCheck(currentNode->next)) {
                return false;
            }
            if(currentNode->val != frontPointer->val) {
                return false;
            }
            frontPointer = frontPointer->next;
        }
        return true;
    }
    bool isPalindrome(ListNode* head) {
        frontPointer = head;
        return recursivelyCheck(head);
    }
};

复杂度分析

• 时间复杂度：O(n)，其中 n 指的是链表的大小。
• 空间复杂度：O(n)，其中 n 指的是链表的大小。

理解计算机是如何运行递归函数的？

我们要理解计算机如何运行递归函数，在一个函数中调用一个函数时，计算机需要在进入被调用函数之前跟踪它在当前函数中的位置（以及任何局部变量的值），通过运行时存放在堆栈中来实现（堆栈帧）。在堆栈中存放好了数据后就可以进入被调用的函数。在完成被调用函数之后，他会弹出堆栈顶部元素，以恢复在进行函数调用之前所在的函数。在进行回文检查之前，递归函数将在堆栈中创建 n 个堆栈帧，计算机会逐个弹出进行处理。所以在使用递归时空间复杂度要考虑堆栈的使用情况。