461. 汉明距离 (opens new window)

题目：

两个整数之间的 汉明距离 (opens new window) 指的是这两个数字对应二进制位不同的位置的数目。

给你两个整数 x 和 y，计算并返回它们之间的汉明距离。

示例：

示例 1：

输入：x = 1, y = 4
输出：2
解释：
1   (0 0 0 1)
4   (0 1 0 0)
       ↑   ↑
上面的箭头指出了对应二进制位不同的位置。

示例 2：

输入：x = 3, y = 1
输出：1

解题：

汉明距离广泛应用于多个领域。在编码理论中用于错误检测，在信息论中量化字符串之间的差异。

两个整数之间的汉明距离是对应位置上数字不同的位数。

根据以上定义，我们使用异或运算，记为 ⊕，当且仅当输入位不同时输出为 1。

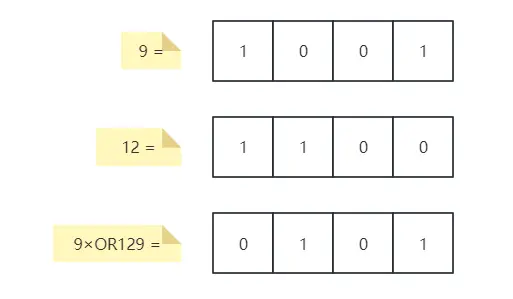
计算 x 和 y 之间的汉明距离，可以先计算 x⊕y，然后统计结果中等于 1 的位数。

现在，原始问题转换为位计数问题。位计数有多种思路，将在下面的方法中介绍。

方法一：内置位计数功能

class Solution {
public:
    int hammingDistance(int x, int y) {
        return __builtin_popcout(x ^ y);
    }
};

复杂度分析

• 时间复杂度：O(1)。不同语言的实现方法不一，我们可以近似认为其时间复杂度为 O(1)。

• 空间复杂度：O(1)。

方法二：移位实现位计数

本方法将使用位运算中移位的操作实现位计数功能。

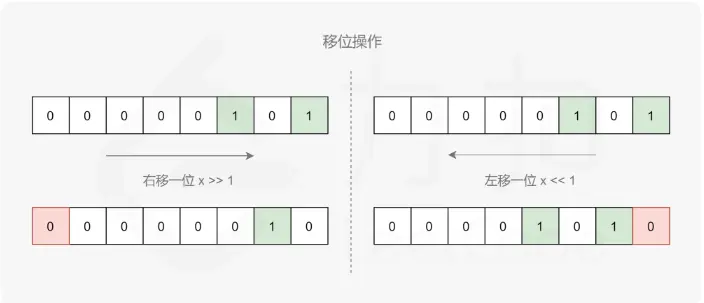
具体地，记 s=x⊕y，我们可以不断地检查 s 的最低位，如果最低位为 1，那么令计数器加一，然后我们令 s 整体右移一位，这样 s 的最低位将被舍去，原本的次低位就变成了新的最低位。我们重复这个过程直到 s=0 为止。这样计数器中就累计了 s 的二进制表示中 1 的数量。

class Solution {
public:
    int hammingDistance(int x, int y) {
        int s = x^y, ret = 0;
        while(s) {
            ret += s & 1;
            s >>= 1;
        }
        return ret;
    }
};